애플, LLM 학습의 스케일링 법칙을 다시 쓰다: Complete(d) Parameterisation

이 글은 arXiv 논문 “Completed Hyperparameter Transfer across Modules, Width, Depth, Batch and Duration”(arXiv:2512.22382)를 토대로 작성되었습니다.

---

대규모 LLM 학습에서 하이퍼파라미터 튜닝은 학습 안정성과 최종 성능을 좌우하지만, 반복 실험 비용이 크다는 한계가 있습니다. 이 논문은 작은 규모에서 찾은 최적의 하이퍼파라미터를 스케일이 달라진 더 큰 모델에도 일관되게 적용할 수 있도록 Complete(d) Parameterisation 관점에서 전이 규칙을 정리합니다.

논문이 확장하는 포인트는 두 가지입니다.

• 스케일 축의 확장: 폭/깊이뿐 아니라 배치 크기와 학습 기간 변화까지 포함해 학습 동역학을 보존
• 탐색 공간의 확장: 전역(global) 설정을 넘어 모듈별(per-module) 하이퍼파라미터 최적화/전이 가능성을 실험적으로 분석

1. 실험 결과: 작게 찾아서 크게 적용한다

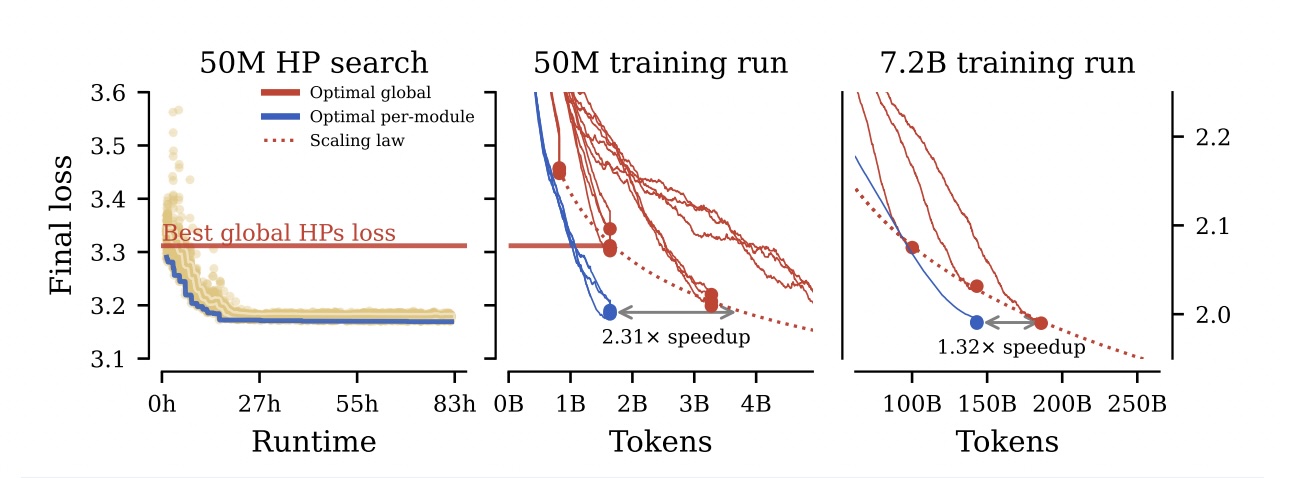
먼저 논문이 보고한 핵심 실험 결과입니다. 저자들은 50M 파라미터의 작은 모델에서 최적의 하이퍼파라미터를 찾은 뒤, 이를 7.2B 모델에 그대로 적용했습니다.

(좌) 50M 모델에서 모듈별 최적화(파란선)가 전역 최적화(빨간선)보다 월등히 빠름을 확인. (우) 이를 7.2B 모델로 전이했을 때도 성능 우위가 유지됨.

보고된 결과:

• 50M 모델 기준: 기존 방식(Global HP) 대비 2.31배 학습 속도 향상
• 7.2B 모델 기준: 추가 튜닝 없이 설정값만 전이했음에도 1.32배 속도 향상

대규모 모델 학습에서 반복적인 하이퍼파라미터 재탐색 비용을 줄일 수 있음을 시사합니다.

2. 핵심 아이디어: 배치 크기/학습 기간이 변해도 학습 동역학 유지

모델 크기를 키울 때 μP(Maximal Update Parametrization)를 사용해 파라미터를 조정하는 것은 이미 알려진 사실입니다. 이 논문은 여기서 더 나아가 배치 크기와 학습 기간이 변할 때도 학습의 안정성을 유지하는 Complete(d) Parameterisation을 제안하죠.

저자들은 학습 과정을 연속적인 시간의 흐름, 즉 확률 미분 방정식(SDE) 관점에서 해석하며, 배치 크기/학습 기간 변화에도 학습 동역학을 보존하기 위한 스케일 규칙을 도출합니다.

2.1. 학습을 SDE로 해석하기

SGD나 AdamW 같은 옵티마이저는 연속적인 확률 과정을 이산적(Discrete) 단계로 근사한 것으로 볼 수 있습니다. 배치 크기가 커지면 그래디언트의 노이즈($\sigma$)가 줄어드는데, 이때 학습의 동역학을 유지하려면 파라미터를 어떻게 조정해야 할까요?

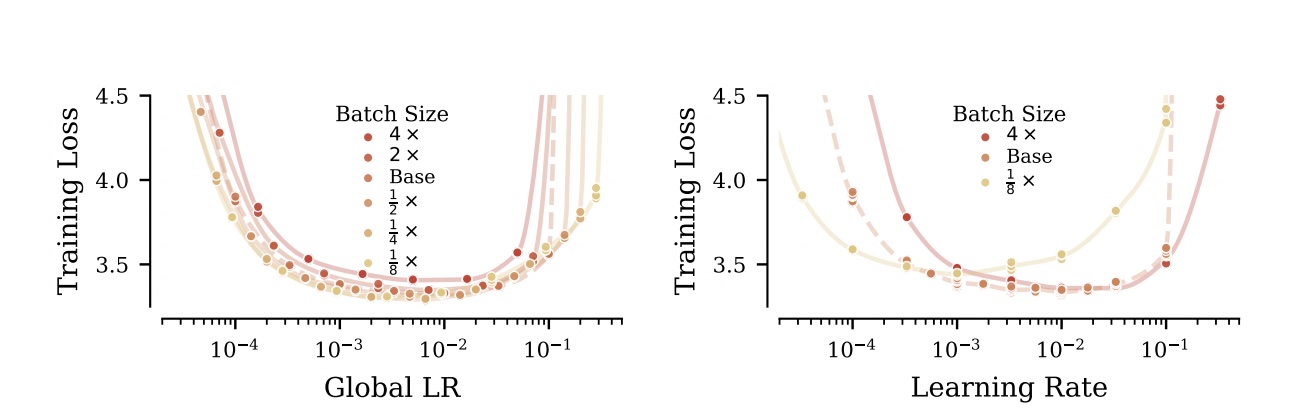
2.2. Square Root Rule

연구진은 수식 유도를 통해, 배치 크기를 $\kappa$배 키울 때 학습률($\eta$)과 가중치 감쇠($\lambda$)를 $\sqrt{\kappa}$배 키워야 한다는 제곱근 비례 규칙을 도출했습니다.

\[\eta' = \sqrt{\kappa}\eta, \quad \lambda' = \sqrt{\kappa}\lambda\]

직관적으로는 배치 크기가 4배 커지면 그래디언트 노이즈 스케일이 2배 감소하므로, 학습률과 가중치 감쇠를 2배로 스케일해도 유사한 학습 동역학을 유지할 수 있다는 해석입니다.

(좌) 제안한 Square Root Rule을 적용하면 배치 크기가 달라도 Loss 곡선이 완벽하게 겹침. (우) 단순 선형 규칙을 적용하면 학습 궤적이 망가짐.

3. Per-Module Optimization: 모듈별 하이퍼파라미터 최적화

일반적으로는 모델 전체에 하나의 학습률을 적용합니다. 레이어/모듈마다 다른 값을 두면 탐색 공간이 급격히 커져, 큰 모델에서 직접 튜닝하기가 현실적으로 어렵기 때문입니다.

저자들은 이 제약을 작은 모델에서 우회합니다. 50M 규모에서는 반복 실험 비용이 상대적으로 낮기 때문에, 모듈 타입별로 서로 다른 설정을 탐색한 뒤 이를 큰 모델로 전이합니다.

3.1. 무엇을 튜닝했나?

모델을 구성하는 텐서 타입별로(Attention QKV, MLP, Layer Norm 등) 서로 다른 학습률과 설정을 적용했습니다. 여기에 깊이에 따른 가중치까지 더해 총 79개의 하이퍼파라미터를 최적화했습니다.

3.2. 결과

모듈별 학습률 조합에 따른 Loss 지형도. 단순 랜덤 탐색으로는 찾기 힘든 좁고 깊은 최적점(파란색 영역)이 존재함.

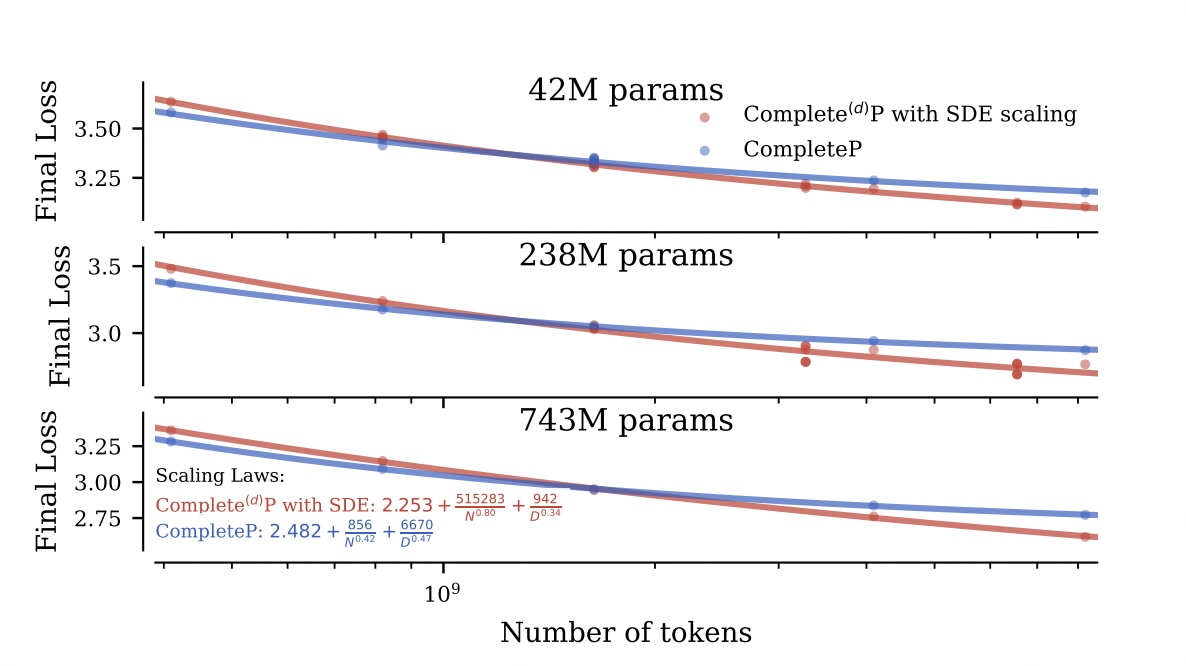
작은 모델에서 찾아낸 모듈별 설정값들은 Complete(d)P 규칙에 따라 7.2B 모델로 변환되었고, 대규모 모델에서도 성능 우위가 유지되는 것으로 보고되었습니다.

4. 결론

이 논문의 메시지는 명확합니다. 하이퍼파라미터 탐색을 작은 모델에서 수행하고, 파라미터화 규칙을 통해 큰 모델로 전이하면, 대규모 학습에서 반복 튜닝 비용을 줄이면서도 안정적인 학습 동역학을 유지할 수 있죠.

• Search Small, Transfer Big: 작은 모델에서 최적 설정을 탐색한 뒤, Complete(d) Parameterisation 규칙으로 큰 모델에 변환/적용
• Architecture of Training: 모델 구조뿐 아니라 학습 설정(폭/깊이/배치/기간/모듈별 HP)을 스케일 축 전반에서 일관되게 설계

Complete(d) Parameterisation과 Square Root Rule은 스케일이 달라져도 비교 가능한 학습을 만들기 위한 실용적인 기준점을 제공합니다.